Donnez du sens
à tous vos feedback clients
Et délivrez une expérience exceptionnelle

Une vision unifiée de vos feedback client
Centralisation de tous vos feedback clients : enquêtes de satisfaction, avis clients et conversations dans 1 seule solution
Analyse poussée avec l’IA
Notre Intelligence Artificielle vous fait gagner un temps précieux pour analyser et comprendre les insights clients
Animation et partage des résultats
Créez une véritable culture client en partageant les retours clients à l’ensemble des collaborateurs
Quel que soit votre besoin,
notre solution peut y répondre
Rassemblez les insights clients, diffusez la culture client
Notre solution vous permet de centraliser l’ensemble de vos feedback clients. Vous avez une vision globale qui vous permet d’aligner vos actions sur les attentes clients et de transformer vos données en leviers de performance avec l’aide de l’IA.
- Une vision client globale, pour des décisions éclairées
- Des insights précis, pour des actions à fort impact
- Un déploiement simple et sécurisé, adapté à vos contraintes
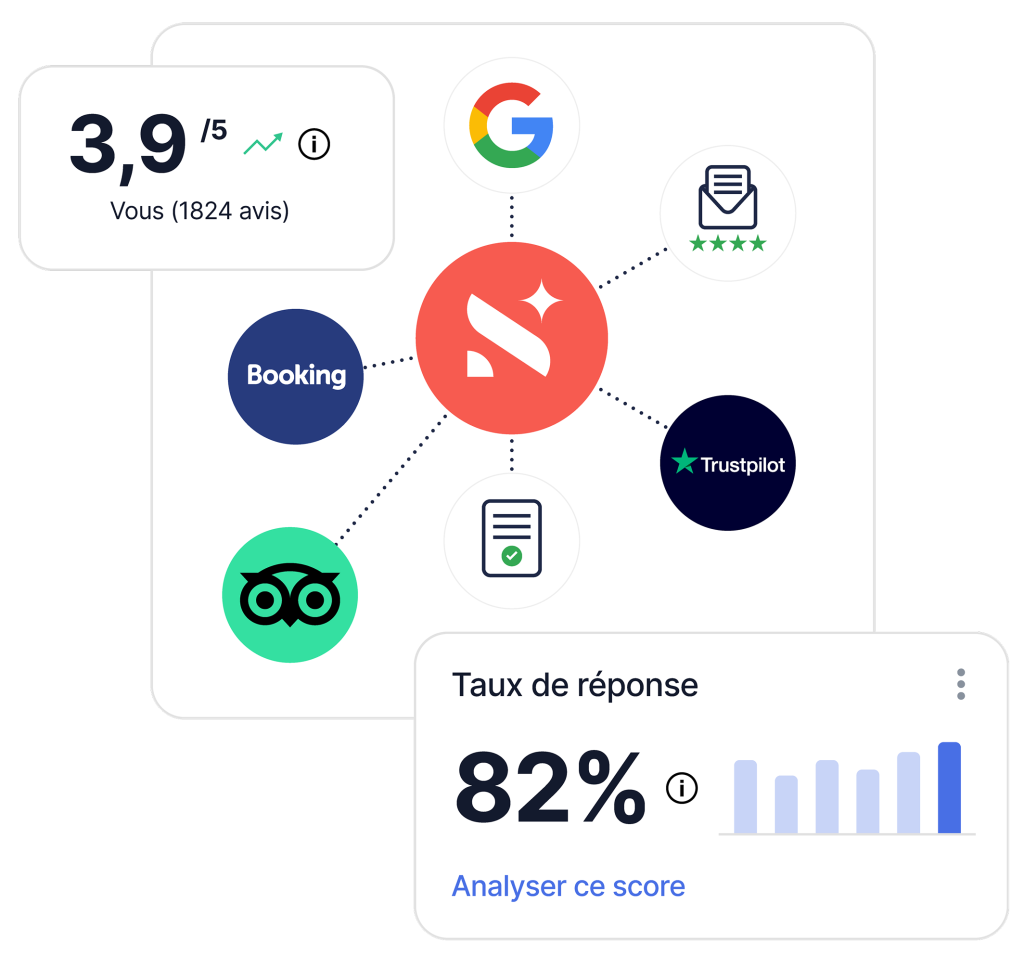
Poussez les analyses, prenez des décisions éclairées
Exploitez l’IA et l’analyse sémantique pour obtenir des insights approfondis, fiables et exploitables, en quelques clics seulement. Transformez les données en plans d’action concrets grâce à des indicateurs clairs et une hiérarchisation automatisée des enjeux.
- Rassemblez toutes vos données, sans effort
- Des analyses précises, pour agir rapidement
- Priorisez vos actions, maximisez votre impact
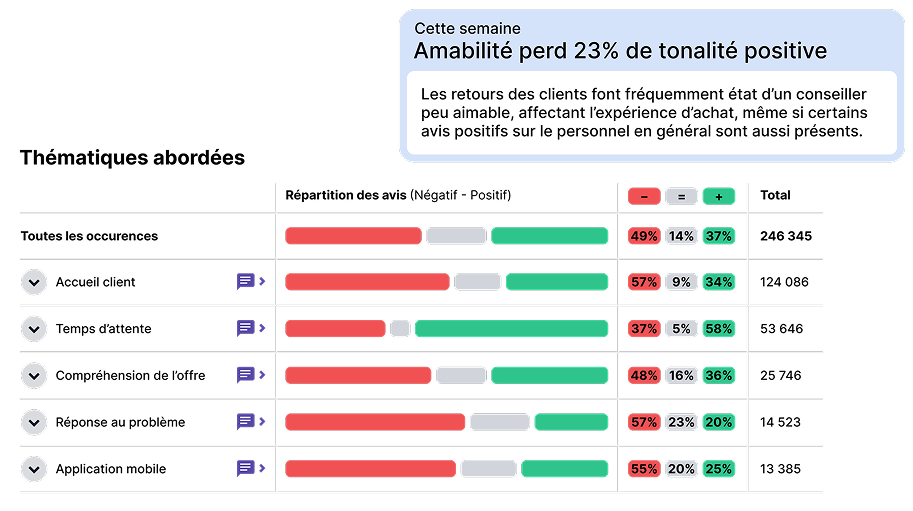
Suivez vos performances, corrigez les insatisfactions
Suivez vos performances en direct, comparez-les à vos objectifs, au réseau et à la concurrence. Partagez-les avec vos équipes pour renforcer l’engagement et gagnez du temps avec l’assistance de l’IA aux réponses aux clients.
- Suivez, comparez, partagez votre performance
- Boostez votre E-réputation
- Répondez mieux, plus vite

Profitez de notre accompagnement
Toutes nos offres intègrent un accompagnement par un Customer Success Manager (CSM).
Votre CSM vous facilite la prise en main de notre solution SaaS ; vous êtes autonome mais vous pouvez compter sur le soutien des équipes de SatisFactory et de leurs 16 ans d’expertise.
Avec la solution Feedback de SatisFactory, les équipes opérationnelles peuvent piloter, analyser la satisfaction de leurs clients en temps réel et ainsi mettre en place des plans d’actions correctifs et d’amélioration continue.
Karine Boudia - Suez
SatisFactory nous a permis de nous rapprocher de nos clients, de mieux comprendre leurs attentes et de pouvoir viser l’excellence opérationnelle.
Claire Dierkens - Auchan
Feedback est un outil puissant qui nous permet de répondre plus facilement et plus rapidement aux retours de nos clients.
Margaux Michelet - AUTOBACS
Les dernières actualités

Concevoir un email d’invitation pour une enquête de satisfaction
Vous souhaitez mesurer la satisfaction de vos clients par rapport à vos produits ou services ? Et comme la majorité des marques vous souhaitez utiliser le canal email, moins cher mais relativement encombré aujourd'hui, pour cela, il faut vous démarquer et capter l'attention de vos clients pour recueillir leur feedback.
vendredi 06 septembre 2024

DMA : Comment l’Union Européenne bouleverse le paysage des avis en ligne
Le domaine du marketing digital est en perpétuelle évolution, façonné par les avancées technologiques et les réglementations en vigueur. Au cœur de cette transformation se trouve le Digital Markets Act (DMA).
jeudi 04 avril 2024

SatisFactory et ConsumerLab s’unissent pour devenir leader du Customer Feedback Management
SatisFactory et ConsumerLab, tous deux éditeurs de solutions SaaS, annoncent leur rapprochement pour déployer des synergies innovantes sous la marque SatisFactory. Celui-ci vise à réinventer le Feedback Management grâce à une expérience utilisateur améliorée.
mercredi 14 février 2024

